温度依存性のキャンセル
ここまでで、電源電圧に依存しない電流をI1とI2のI-Vカーブの交点で決めることができることができました。
そのときの電流$I_0$は絶対温度に比例します。これを一般にPTAT(Proportional To Absolute Temperature)電流といいます。
以下で$I_0$がPTATとなることを計算してみます。
BJTの電流式は
$$I_{s}\exp{\frac{qV_{BE}}{kT}}\tag{1}$$
ここで$q$は電気素量、$k$はボルツマン定数、$T$は温度、$I_s$はBJTの飽和電流で温度の関数です。
これをもとに、M1に流れる電流とM2に流れる電流、抵抗に流れる電流が等しいとして以下の連立方程式を解けば求まります。
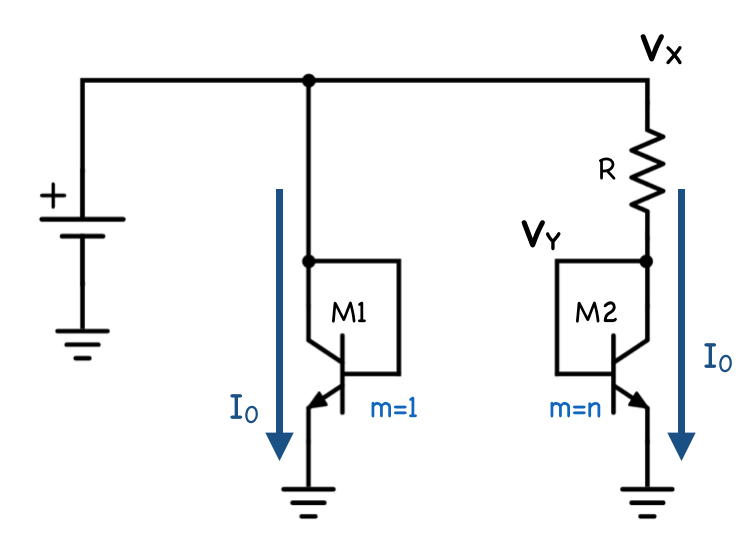
\begin{cases}
I_0 = I_s \exp^{\frac{qV_{X}}{kT}} & \\
I_0 = nI_s \exp^{\frac{qV_{Y}}{kT}} & \\
I_0 = \frac{V_X – V_Y}{R} & \tag{2}
\end{cases}
これを解くと、
$$I_0 = \frac{kT}{qR}\log{n}\tag{3}$$
となりPTAT電流の式が得られます。
この式から電流値は抵抗に反比例し、$I_0$に依存しないことがわかります(シミュレーションしてみると、実際にはBJTのプロセス依存があります)。
また、温度係数は正となることもわかります。
このPTAT電流を直接回路のバイアス電流として利用することもありますが、
ここでのBGRとしては、BJTと抵抗に流すことで温度依存のない電圧を生成します。
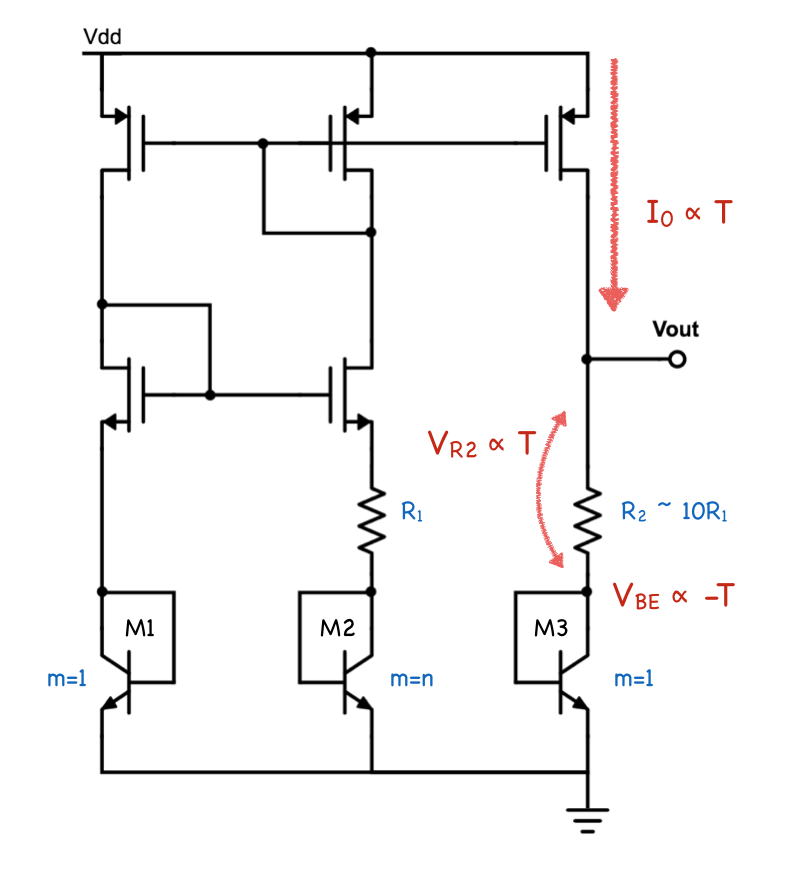
細かい計算は省きますが、電流一定のもと式(1)を$V_{BE}$について解いて温度で微分すると温度係数は、
$$\frac{\partial V_{BE}}{\partial T} = \frac{V_{BE}-(4+m)V_{T}-E_{g}/q}{T}\tag{4}$$
となります(Behzad Razavi, アナログCMOS集積回路の設計 応用編)。
温度係数は温度$T$や$V_{BE}$自体の関数なので綺麗な比例関係とはならず定量的な計算が難しいのですが、重要なのはこの温度係数は負となるということです。
一方で、式(3)から抵抗$R_2$に流れる電流は温度に比例して増加するので、両端での電圧$V_{R_2}$は温度に正に比例することになります。
$$V_{R_2} = \frac{kTR_2}{qR_1}\log{n}\tag{5}$$
BGRの出力電圧$V_{out}$は$V_{BE}$と$V_{R_2}$の和になるので、$V_{R_2}$の温度係数が$V_{BE}$の温度係数をキャンセルするように、抵抗$R_2$を調整することで温度に依らない出力電圧$V_{out}$を生成することができます。
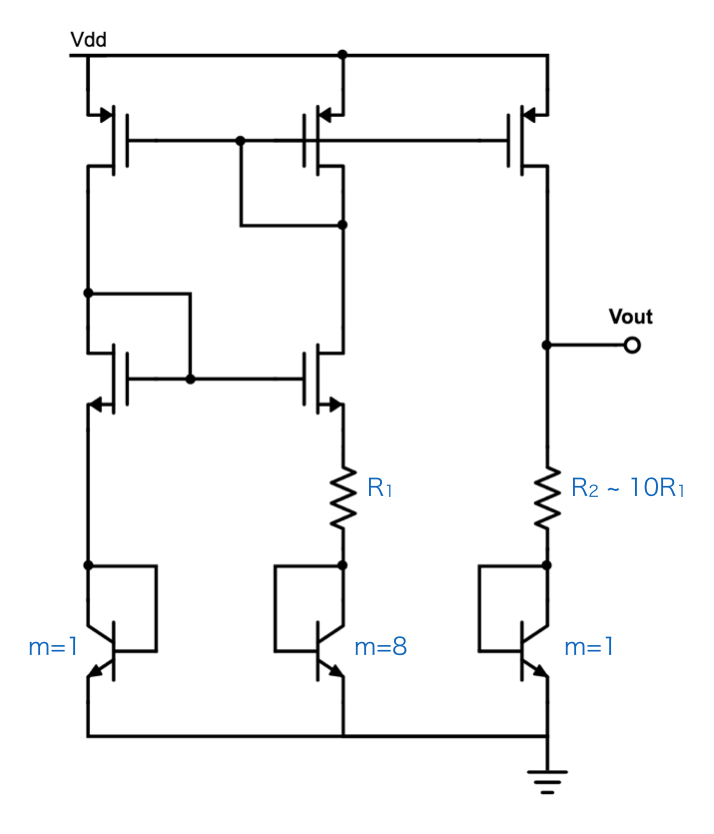
プロセス依存性のキャンセル
集積回路内の抵抗やBJTは製造工程の不均一によって回路特性がばらつきます。ばらつきにはウェハ上でならだかに変化する大域ばらつきと、個々の素子毎にばらつく局所ばらつきがあります。このうち局所ばらつきは素子毎にランダムなので基本的にキャンセルできませんが(キャリブレーションという手はあります)、大域ばらつきは回路構成次第でキャンセル可能です。
特に、集積回路上の抵抗素子の大域ばらつきは大きく、抵抗値が$\pm 10\%$以上ばらついてしまうことがあります。
BGRではこのばらつきをキャンセルすることができます。
式(5)から分かるように、もし大域ばらつきによって抵抗値が設計値よりも$+10\%$大きくなったとしても、$V_{R_2}$は$R_1$と$R_2$の比の関数なので、$V_{R_2}$の値は変わらずばらつきの影響を受けません。
BJTのばらつきもBGRの出力電圧に影響を及ぼしますが、BJTのより正確なモデルを用意する必要があるようで定量化は難しいようです。
シミュレーション上では、ばらつきによって$I_s$が大きい($V_{BE}$が小さい)と$I_0$も大きくなり、$V_{R_2}$と$V_{BE}$でキャンセルするように設計が可能ですが、上述した式からは説明することはできません。
いずれにせよ、実設計では温度依存性やプロセス依存性などはシミュレーションにて確認を行い細かく調整していく必要があります。

コメント