アナログ回路設計において利得は重要な設計パラメータの一つです。
ここでは利得の定義の定義について確認したあと、ソース接地増幅段とソースフォロワの小信号利得を導出してみます。
利得(gain)
大信号における利得の定義は以下の通りです。
大信号解析で得られた入力と出力の関係式について微分することで、バイアス点ごとの利得を計算することができます。
$$A_v=\frac{\partial V_{out}}{\partial V_{in}}$$
あるいは小信号では単に、
$$A_v=\frac{V_{out}}{V_{in}}$$
と書きます。
小信号では入力と出力は比例関係にあり、その比例係数が利得ということになります。
例1:ソース接地増幅段(抵抗負荷)(common-source amplifier)
最初の例として最も基本的な増幅段である抵抗負荷のソース接地回路の利得を求めてみます。
ソース接地回路は入力がゲート、出力がドレインの構成です。
MOSFETは飽和領域で動作するよう設計されます。
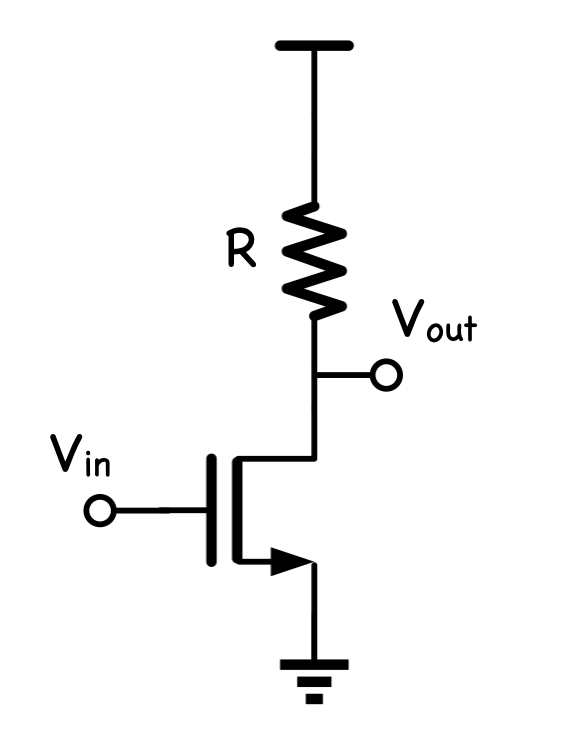
この回路の小信号等価回路は以下のようになります。
ただしまだ不要な部分を残しています。
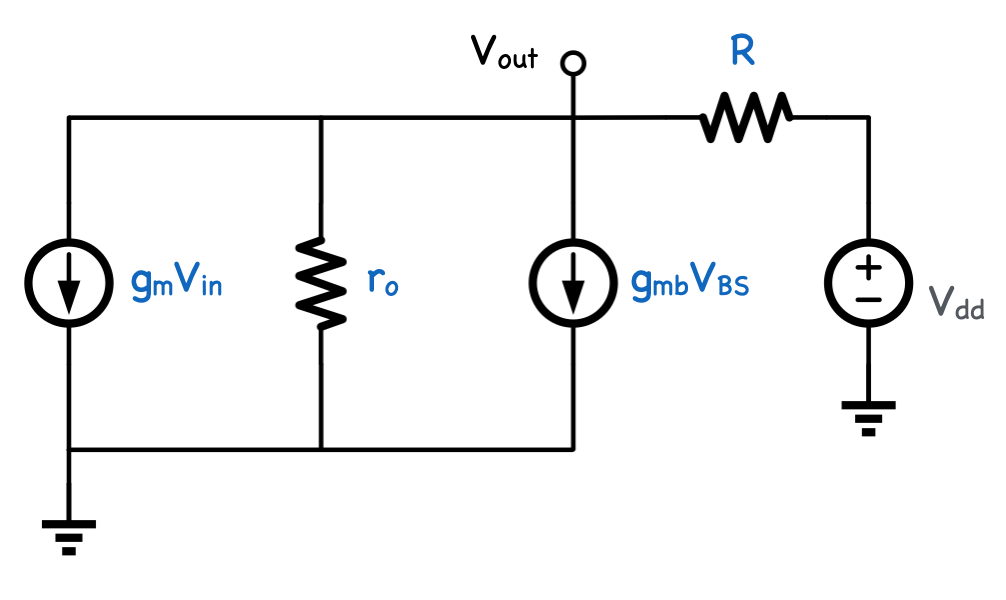
$V_{BS}$は変化しないので定電流源として扱うことができます。したがって開放(open)とすれば良いです。
また、定電圧源は短絡できるので、電源電圧を供給している箇所はグラウンドに接続できます。
これらを反映させると下図左のようにより簡単な回路にできます。
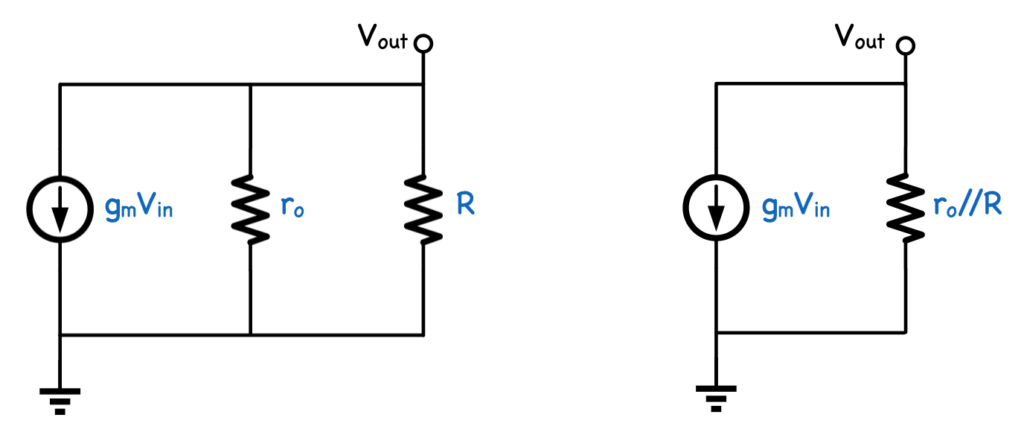
$r_o$と$R$は$V_{out}$とグラウンド間の並列抵抗なのでこれらを一つにまとめると上図右のように非常に簡単な回路図にまとめられます。
電流の向きに注意してオームの法則から$V_{out}$を求めると、
\begin{eqnarray}
V_{out}&=&-g_mV_{in}\cdot (r_o\parallel R) & \\
&=&-g_mV_{in}\frac{r_o R}{r_o+R}
\end{eqnarray}
多くの場合、$r_o$の値は大きいので$r_o \gg R$が成り立ち、利得は単に
$$A_v=\frac{V_{out}}{V_{in}}=-g_mR$$
と書けます。
一方で、$R$に対してMOSFETのチャネル長変調効果$r_o$が並列に見えてしまうので、どれだけ$R$を大きくしても利得を$g_mr_o$より大きくすることはできません。これをMOSFETの固有利得と言います。
例2:ソースフォロワ(source follower)
ソースフォロワは小信号利得がほぼ1の回路です。
増幅も減衰もしないこの回路の用途は電圧のレベルシフトだったり、あるいは負荷インピーダンスの調整で、アナログ回路設計においてしばしば使用されます。
下図左のように入力がM1のゲート、出力がM1のソースで、
M2が電流源として電流を決めています。
全てのMOSFETは飽和領域で動作させ、基板はグラウンドに接続しているとします。
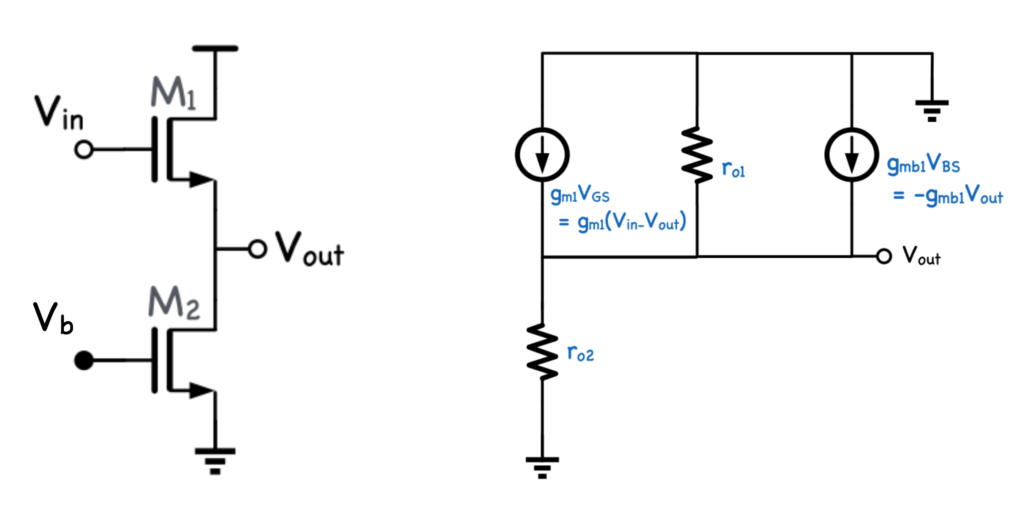
M1のソースが基板電位に対して変動するので基板バイアス効果($g_{mb}$)を考慮する必要があります。
今回のケースでは、$V_{out}$に比例した電流を$V_{out}$からグラウンドに流すので抵抗で置き換えることが可能です(下図左)。
さらに並列抵抗を一つにまとめると下図右のようになります。
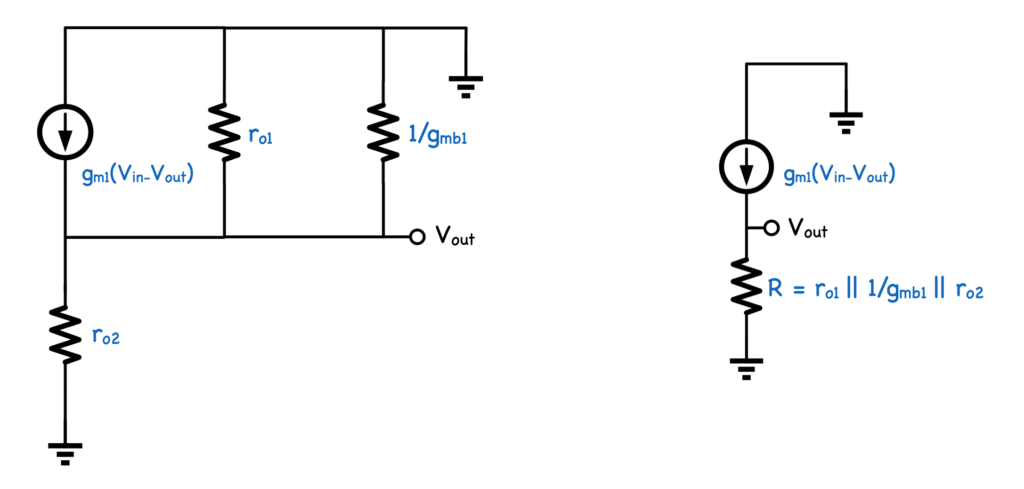
オームの法則から、
$$V_{out}=g_{m1}(V_{in}-V_{out}) \cdot R$$
となり利得は
$$A_v=\frac{g_{m1}R}{1+g_{m1}R}$$
となります。
ここで、
$$R=r_{o1}\parallel g_{mb1}^{-1} \parallel r_{o2}$$
としました。
式からわかるように、$g_{m1}R$が大きいほど利得は1近づきます。
実際の設計では利得を高く維持するためにM1のソースと基板をショートさせて基板バイアス効果による抵抗低下を防いだり、電流源はカスコード構成にして高抵抗にすることが多いです。

コメント